Regelen met PID
Waarom zou je als thuisbrouwer een aparte pagina over PID regelaars nodig hebben? Als je een RIMS / HERMS installatie hebt en je koopt een kant en klare PID regelaar, die alles voor zijn rekening neemt, waarom zou je dan nog moeilijk doen over een PID regelaar? Ook als thuisbrouwer moet je echter een idee hebben hoe een PID regelaar werkt, omdat je zelfs met een kant-en-klaar apparaat makkelijk een verkeerde instelling kunt realiseren, wat kan leiden tot een flink temperatuur doorschot of een te langzame responsie. Je zou ook kunnen bedenken dat je geen regelaar nodig hebt, je zet gewoon de brander uit wanneer de temperatuur bereikt is. Wat je zult zien met zo'n "regeling" is dat er een behoorlijk temperatuur doorschot optreedt. De brander moet geleidelijk aan uitgezet gaan worden, lang voordat de gewenste temperatuur bereikt is. En dat is waarvoor je zo'n regelaar nodig hebt. En een PID regelaar is dan de meest gebruikte regelaar.
PID staat voor Proportioneel, Integrerend en Differentiërend. Als je in het binnenste kijkt van een PID regelaar, dan zie je dat het daadwerkelijk bestaat uit drie paden. Het was heel gebruikelijk om zo'n PID regelaar op te bouwen met discrete elektronica, maar tegenwoordig is iedere PID regelaar in software gerealiseerd, we spreken dan ook van een digitale PID regelaar. Zo'n softwarematige PID regelaar zit ook in de kant en klare kastjes die je kunt kopen. En als je deze pagina in zijn geheel bestudeerd hebt, dan moet je constateren dat je erg veel geld moet betalen voor die paar regels code (Zelfbouw kan dus lonend zijn)! Op deze pagina probeer ik de volgende zaken uit te leggen:
- 1. Basiskennis Regelen met PID: enkele basisbegrippen die noodzakelijk zijn om de rest van het verhaal te begrijpen.
- 2. Implementatie van een PID regelaar: een echte PID regelaar met (pseudo) C broncode
- 3. Instellen van een PID regelaar: het vinden van een optimale set parameters voor het brouwsysteem. Deze paragraaf bestaat wederom uit de volgende deelparagrafen:
Wil je na het lezen van dit verhaal zelf je eigen PID regelaar maken, kijk dan met name op de pagina hardware. Hier wordt het complete ontwerp en bouw van een brouwsysteem uitgelegd.
1. Basiskennis Regelen met PID
De belangrijkste componenten van een PID regellus zijn weergegeven in onderstaande figuur.
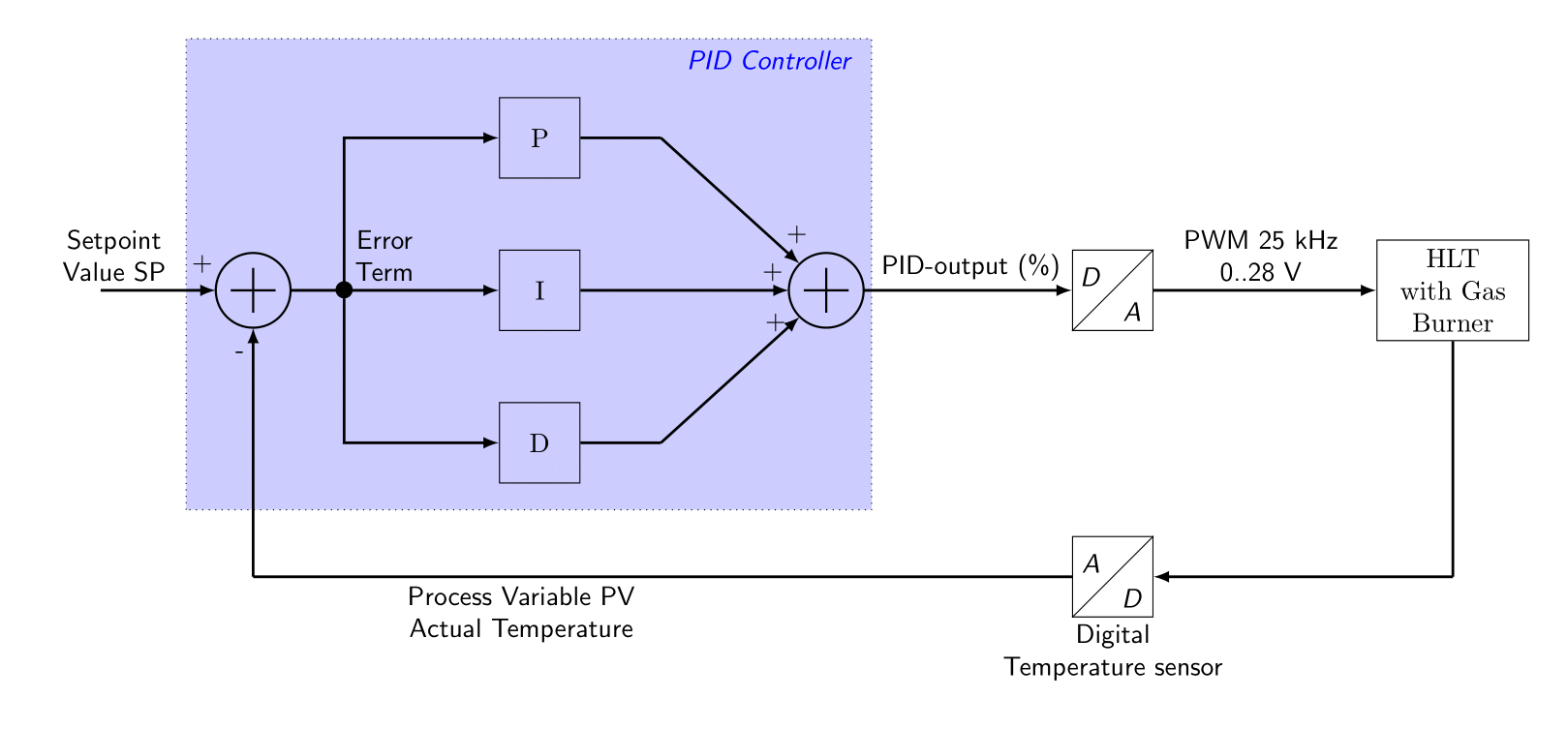
- Process variable: een gemeten waarde van een fysieke grootheid. In de brouwinstallatie is dit de actuele warmwaterketel (HLT) temperatuur.
- Setpoint value: De gewenste referentiewaarde voor de proces variabele. In de brouwinstallatie is de setpoint-value afgeleid van het maischschema. Als een bepaalde maischrust afgelopen is, dan wordt de setpoint-value gelijk gemaakt aan de volgende, hogere, maisch referentietemperatuur.
- Error Term: de foutwaarde, het wiskundige verschil tussen de proces variabele en de setpoint value. Dit is de fout in de regellus die de PID regelaar probeert weg te werken. Deze foutwaarde is 0 wanneer de actuele temperatuur gelijk is aan de gewenste temperatuur. Een goed ingestelde regellus is in staat om een kleine foutwaarde te realiseren en vast te houden.
- PID-Output: De output van de PID regelaar, dit is een waarde tussen 0 % en 100 %. Dit signaal bepaalt hoever de brander open gezet gaat worden.
- D/A: Digitaal naar Analoog Omzetter (DAC). Dit blokje zet het digitale signaal om in een analoog signaal. In het brouwsysteem gebeurt dit met een timer die een PWM signaal afgeeft. Het opgewekte signaal heeft een frequentie van ongeveer 25 kHz, de brouwelektronica zet het 0..5 Volt PWM signaal om in een 0..28 Volt PWM signaal, dat op de gasklep van de brander gezet wordt.
- A/D: Analoog naar Digitaal Omzetter (ADC). Dit blokje zet het analoge signaal om in een digitale versie. Het brouwsysteem gebruikt een digitale temperatuursensor LM92, die een ingebouwde A/D omzetter heeft. Hierdoor is geen aparte A/D omzetter meer nodig.
Het Proportioneel-Integrerend-Differentiërend (PID) algoritme wordt zeer veel gebruikt in de meet- en regeltechniek en in de procesautomatisering. De PID methode is makkelijk te realiseren in elektronica, dat kan zowel in hardware als in software. Het brouwprogramma kent een aparte software routine, geschreven in de programmeertaal C++, die de PID regelaar implementeert. Er zijn twee soorten basisvormen voor PID regelaars:
- PID Positie Algoritme: De output van de regelaar bepaalt direct de uitsturing (positie) van het verwarmingselement. De output is dan ook een absolute waarde. Voorbeeld: de output van de regelaar is 5 %, het verwarmingselement wordt dan ook 5 % van de tijd aan gezet.
- PID Snelheids Algoritme: De output van de regelaar bepaalt de mate van verandering (snelheid) waarmee het verwarmingselement aan of uit gezet wordt. De output is dan ook een relatieve waarde. Voorbeeld: de output van de regelaar is 5 % en de vorige waarde van de regelaar output was 55 %. De nieuwe output waarde van de regelaar zal dan 55 % - 5 % = 50 % bedragen. Het verwarmingselement wordt dan 50 % van de tijd aan gezet.
De implementatie, zoals deze gekozen is voor het brouwprogramma, is die van het PID snelheids algoritme. Dit algoritme wordt ook in de meeste digitale PID regelaars gebruikt.
Een andere belangrijke eigenschap van een regellus is of deze inverterend of niet-inverterend werkt:
- Niet-inverterende Loop: het proces kent een positieve versterking, dit houdt in dat wanneer de output van de PID regelaar verhoogd wordt, de proces variabele (de temperatuur) ook groter zal worden. In onze brouwinstallatie is dus sprake van een niet-inverterende loop.
- Inverterende Loop: het proces kent een negatieve versterking, dit houdt in dat wanneer de output van de PID regelaar verhoogd wordt, de proces variabele (de temperatuur) juist kleiner zal worden. Zo'n loop komt vaak voor in koelsystemen, waar een hogere regelaarwaarde leidt tot meer koeling. Daarom worden deze loops soms ook wel koeling-loops genoemd.
In bovenstaande figuur waren er drie parallelle paden te zien in de PID regelaar:
- Proportioneel: De proportionele term reageert direct op de grootte van de fout. De proportionele term wordt berekend door de Kc parameter te vermenigvuldigen met de foutwaarde. Wanneer deze error term nul is, zal de proportionele term ook nul zijn.
- Integrerend: De integrator (of reset) term integreert (sommeert) de foutwaarden. Vanaf de eerste aanroep van de PID regelaar (nadat deze vrijgegeven is), zal de integrator een lopende som bijhouden van alle foutwaarden.
- Differentiërend: De differentiërende term reageert op veranderingen in de foutwaarde (t.o.v. de vorige foutwaarde). De taak van deze term is om te anticiperen op een mogelijke groei van de foutwaarde om hierop de output van de regelaar op voorhand aan te passen.
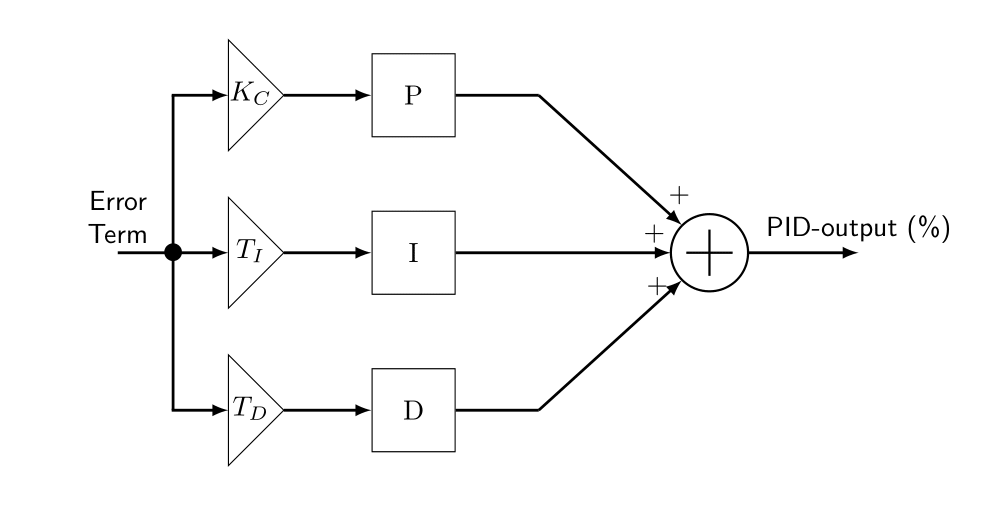
De P, I en D termen werken samen als een team. Om iedere term afzonderlijk te kunnen controleren, wordt iedere term uitgerust met een instelbare parameter:
- Kc: De proportionele versterking. In sommige literatuur wordt deze versterking ook wel Kp genoemd. De eenheid hiervan is (voor onze brouwinstallatie) is % / °C.
- Ti: De tijdconstante voor de integrerende term. In sommige literatuur wordt deze term gedefinieerd als: Ti = Kc / Ki. De eenheid hiervan is seconde.
- Td: De tijdconstante voor de differentiërende term. In sommige literatuur wordt deze term gedefinieerd als: Td = Kc / Kd. De eenheid hiervan is seconde.
- In feite is er nog een vierde parameter die van belang is en dat is de sample tijd Ts. De sample tijd Ts is gedefinieerd als de tijd tussen twee aanroepen naar de PID regelaar. In onze brouwinstallatie is die sample tijd Ts voor de PID regelaar gelijk aan 30 seconden (hetgeen betekent dat 1 keer per 30 seconden een nieuwe waarde voor de output van de PID regelaar wordt bepaald).
Er is nog 1 aanvullende opmerking te maken en die betreft het type PID regelaar (voor details zie wederom het document PID controller Calculus with full C source):
- Type A PID Regelaar: Dit is het type PID regelaar dat in de figuur hierboven staat. Deze vorm heet ook wel Tekstboek PID. Niet veel ontwerpers vinden dit een goede implementatievorm, voornamelijk omdat de D term ook afhangt van de foutwaarde. En omdat de foutwaarde gelijk is aan het verschil tussen de referentie (setpoint value) en de gemeten waarde (proces variabele), is deze dus ook afhankelijk van de referentie. Een wijziging van de referentie, zal dus ook leiden tot een reactie van de PID regelaar, hetgeen niet de bedoeling is.
- Type B PID Regelaar: In een type B PID controller is de referentie verwijderd uit de D term. Dit leidt dus tot een implementatie waarin de D term alleen nog maar afhangt van de proces variabele (de actuele HLT temperatuur) en niet langer meer van de foutwaarde.
- Type C PID Regelaar: Het type B PID regelaar kan verder verbeterd worden door de foutwaarde ook uit de P term te halen. In een type C regelaar wordt de foutwaarde alleen nog maar naar de I-term gevoerd, maar de P- en D-termen zijn alleen nog maar afhankelijk van de proces variabele (de actuele HLT temperatuur).
Bij sommige industriële PID regelaars kun je het type instellen. Maar als er een type C PID regelaar aanwezig is, dan verdient het de voorkeur om deze te kiezen. Een systeemblokdiagram van zo'n type-C regelaar zie je in onderstaande figuur. Duidelijk zijn de P, I en D-acties te zien. Dit is ook de regelaar die in het brouwsysteem gebruikt wordt.
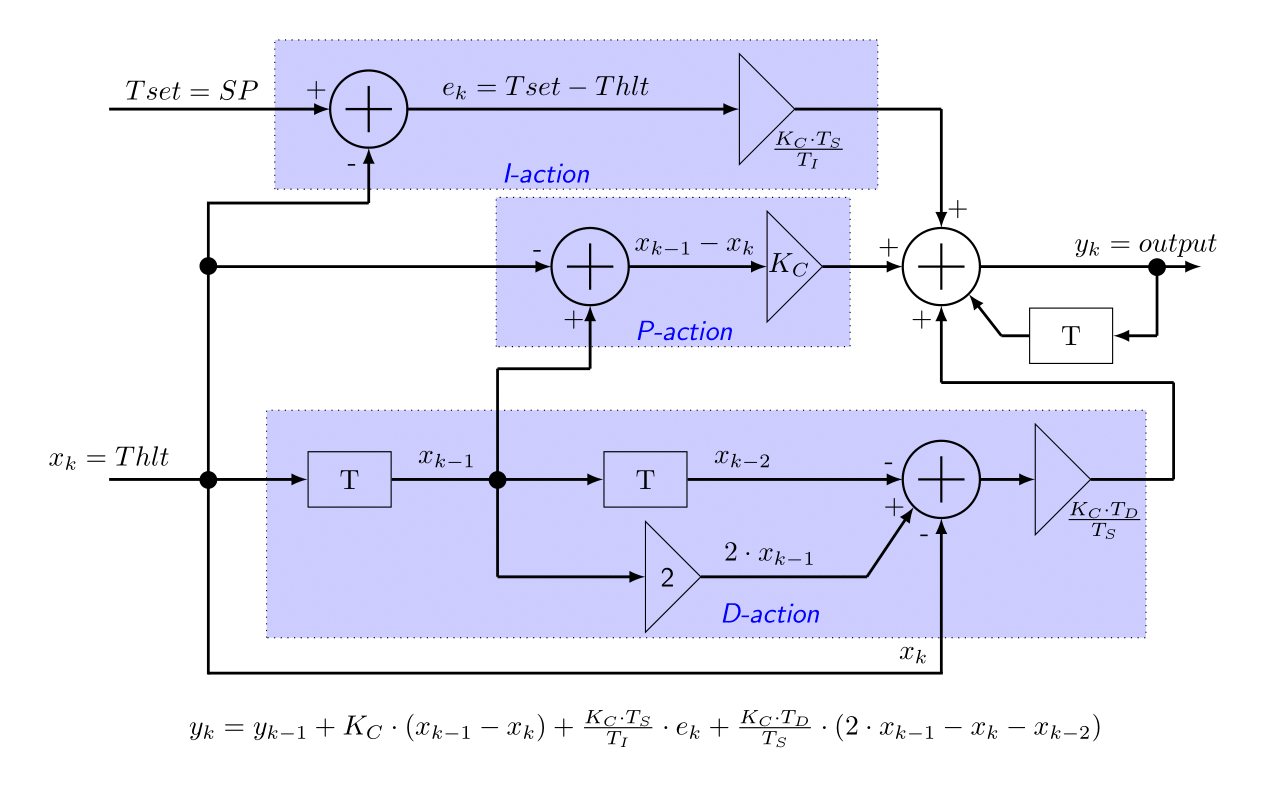 Terug naar boven
Terug naar boven
2. Implementatie van een PID regelaar
Er zijn vele verschillende manieren om een PID regelaar te implementeren. In feite kent iedere moderne PLC een of meerdere implementatievormen van een PID regelaar, die vaak onderling weer verschillend zijn. Dit is bij het bouwen van je eigen regelaar vaak verwarrend (welke implementatie moeten we kiezen?). De afleiding van een vorm, die geschikt is voor implementatie in software, is nogal wiskundig van aard (Z-transformaties). Die wiskundige afleiding heb ik niet op deze pagina staan, maar wel in een apart document gezet. In dit document staat direct ook de volledige C source code gegeven, zodat je hiermee direct je eigen regelaar kunt bouwen. Ben je hierin geïnteresseerd, lees dan dit document: PID Controller Calculus with full C source. Aan de andere kant, als de wiskundige kant je niet echt boeit en je meer geïnteresseerd bent hoe je zelf zo'n regelaar kunt maken, dan moet je de rest van dit verhaal zeker doornemen. Ik heb hier gekozen voor een PID regelaar die volgens het PID snelheids algoritme werkt, die een Type C regelaar is, die niet-inverterend werkt en zonder filtering van de D-actie. Dit is een zogeheten Takahashi regelaar en is de beste manier om een PID regelaar daadwerkelijk te implementeren. Onderstaande figuur laat de C code hiervan zien. Deze figuur maakt hopelijk duidelijk hoe je je eigen regelaar kunt maken in je favoriete programmeertaal (de grijze regels zijn commentaar).
/*==================================================================
Function name: pidInit(), pidCtrl()
Author : Emile
------------------------------------------------------------------
Purpose : This file contains the main body of the PID controller.
For design details, please read the Word document
"PID Controller Calculus".
In the GUI, the following parameters can be changed:
Kc: The controller gain
Ti: Time-constant for the Integral Gain
Td: Time-constant for the Derivative Gain
Ts: The sample period [seconds]
==================================================================*/
#include "pid_reg_web.h"
#include
void pidInit(pidPars *p, double Kc, double Ti, double Td, double Ts)
/*------------------------------------------------------------------
Purpose : This function initialises the PID controller.
Variables: p : pointer to struct containing PID parameters
Kc: the controller gain [%/C]
Ti: integral time-constant [sec.]
Td: differential time-constant [sec.]
Ts: sample-time period [sec.]
Kc.Ts
ki = ----- (for I-term)
Ti
Td
kd = Kc . -- (for D-term)
Ts
Returns : No values are returned
------------------------------------------------------------------*/
{
p->kp = Kc;
if (Ti < 1e-3)
p->ki = 0.0;
else p->ki = Kc * Ts / Ti;
if (Ts < 1e-3)
p->kd = 0.0;
else p->kd = Kc * Td / Ts;
p->xk_2 = p->xk_1 = p->yk = 0.0;
} // pidInit()
double pidCtrl(double xk, double tset, pidPars *p, int vrg)
/*------------------------------------------------------------------
Purpose : This function implements the Takahashi Type C PID
controller: the P and D term are no longer dependent
on the set-point, only on PV (which is Thlt).
This function should be called once every TS seconds.
Variables:
xk : The input variable x[k] (= measured temperature)
tset : The setpoint value for the temperature
*p : Pointer to struct containing PID parameters
vrg: Release signal: 1 = Start control, 0 = disable PID controller
Returns : yk : PID controller output y[k] in % [0..100]
------------------------------------------------------------------*/
{
if (vrg)
{
//--------------------------------------------------------------------------------
// Takahashi Type C PID controller (NO filtering of D-action):
//
// Kc.Ts Kc.Td
// y[k] = y[k-1] + Kc.(x[k-1]-x[k]) + -----.e[k] + -----.(2.x[k-1]-x[k]-x[k-2])
// Ti Ts
//
//--------------------------------------------------------------------------------
p->pp = p->kp * (p->xk_1 - xk); // Kc.(x[k-1]-x[k])
p->pi = p->ki * (tset - xk); // (Kc.Ts/Ti).e[k]
p->pd = p->kd * (2.0 * p->xk_1 - xk - p->xk_2); // (Kc.Td/Ts).(2.x[k-1]-x[k]-x[k-2])
p->yk += p->pp + p->pi + p->pd; // add y[k-1] + P, I & D actions to y[k]
}
else { p->yk = p->pp = p->pi = p->pd = 0.0; }
p->xk_2 = p->xk_1; // x[k-2] = x[k-1]
p->xk_1 = xk; // x[k-1] = x[k]
// limit y[k] to a maximum and a minimum
if (p->yk > PID_OUT_HLIM)
{
p->yk = PID_OUT_HLIM;
}
else if (p->yk < PID_OUT_LLIM)
{
p->yk = PID_OUT_LLIM;
} // else
return p->yk;
} // pidCtrl()
Over de implementatie van zo'n PID regelaar zijn nog een paar opmerkingen te maken:
- Deze code voor de PID regelaar moet iedere TS seconde aangeroepen worden (TS is 20 seconden in mijn brouwprogramma). Dit betekent dat de PID regelaar iedere 20 seconden een nieuwe output waarde berekent.
- De actuele temperatuur wordt iedere seconde uitgelezen. Deze temperaturen worden vervolgens gefilterd en aan deze functie doorgegeven (als xk).
- De waarden voor Kc, Ti, Td en Ts kunnen door de brouwer aangepast worden (zie de GUI sectie op de software pagina).
- De toevoeging _1 bij verschillende variabelen (bijv. xk_1) geeft aan dat dit de voorgaande waarde is van die variabele. Bijv. xk_1 betekent dat dit de waarde van xk tijdens de vorige aanroep van deze functie (20 seconden terug dus). Hetzelfde geldt voor de toevoeging _2 (dat was de waarde 2 * 20 seconden terug).
- Voordat de routine pidCtrl() voor deze eerste keer aangeroepen wordt, moet deze worden geïnitialiseerd. Hiervoor heb ik de pidInit() functie geschreven, die de waarden van de diverse constanten berekent. Deze routine moet dus iedere keer aangeroepen worden wanneer parameters gewijzigd zijn.
- De code hieronder is geschreven in de C programmeertaal. Er is ook een C++ versie van en die wordt gebruikt in het brouwprogramma. Deze is te vinden in de github repository in de bestanden controlobjects.cpp en controlobjects.h
Ik hoor graag van je of je deze listing makkelijk of moeilijk te lezen vond!
Bij deze C code hoort ook een header file (.h file) die de belangrijkste definities en de functie-prototypes bevatten. Wil je deze functies gebruiken, dan volstaat het veelal om de header file te includen in je C project.
#ifndef PID_REG_H
#define PID_REG_H
/*==================================================================
File name : pid_reg_web.h
Author : Emile
------------------------------------------------------------------
Purpose : This is the header file for pid_reg_web.c
==================================================================*/
#define PID_OUT_HLIM (100.0) /* PID Controller Upper limit (%) */
#define PID_OUT_LLIM (0.0) /* PID Controller Lower limit (%) */
//------------------------------------------------------------
// By using a struct for every PID controller, you can have
// more than 1 PID controller in your program.
//------------------------------------------------------------
typedef struct _pidPars
{
double kp; // Internal Kp value
double ki; // Internal Ki value
double kd; // Internal Kd value
double pp; // debug value for monitoring of P-action
double pi; // debug value for monitoring of I-action
double pd; // debug value for monitoring of D-action
double yk; // y[k] , value of controller output (%)
double xk_1; // x[k-1], previous value of the input variable x[k] (= measured temperature)
double xk_2; // x[k-2], previous value of x[k-1] (= measured temperature)
} pidPars; // struct pidParams
//----------------------
// Function Prototypes
//----------------------
void pidInit(pidPars *p, double Kc, double Ti, double Td, double Ts);
double pidCtrl(double xk, double tset, pidPars *p, int vrg);
#endif
Als voorbeeld hoe deze routines aan te roepen zijn vanuit een standaard C-programma, wordt hier onderstaande code weergegeven. De routine pidInit() wordt als eerste aangeroepen met de juiste PID parameters en daarna wordt de regelaar zelf (de routine pidCtrl()) aangeroepen. De routine pidCtrl() heeft de actuele temperatuur nodig, de setpoint waarde, de struct met parameters en een vrijgave signaal. De regelaar zal pas echt gaan regelen, wanneer dit vrijgave signaal een 1 is geworden.
#include
#include
#include "pid_reg_web.h"
int main()
{
pidPars p; // Create a struct for pidPars
double out = 0.0; // PID controller output
double temp = 30.0; // Actual temperature
double sp = 32.0; // Setpoint temperature
// Call pidInit with the proper control parameters
pidInit(&p, 80.0, 280.0, 45.0, 20.0); // p, Kc, Ti, Td, Ts
// Call the actual controller every Ts seconds
out = pidCtrl(temp, sp, &p, 0); // x[k], SP, p, vrg
out = pidCtrl(temp, sp, &p, 0); // call this function every Ts seconds
// The PID-controller is enabled by setting vrg to 1
out = pidCtrl(temp, sp, &p, 1); // Controller is released
out = pidCtrl(temp, sp, &p, 1); //
return 0;
} // main()
3. Instellen van een PID regelaar
Het instellen van de PID regelaar omvat het vinden van zodanige waarden voor Kc, Ti en Td, dat de PID regelaar snel reageert op veranderingen in de referentie temperatuur en/of de gemeten temperatuur, waarbij de temperatuur doorschot wordt geminimaliseerd. Het instellen of tunen van een PID regelaar is altijd nodig, of je nu een kant en klare regelaar gekocht hebt, of dat je er zelf eentje gemaakt hebt. Het voordeel van zo'n kant en klare regelaar is dat ze vaak een auto-setup functie bevatten, die de optimale parameterwaarden automatisch voor je vindt (meestal dan...). Maar zelfs zo'n kant en klare regelaar gebruikt dezelfde algoritmen als die ik hier beschrijf. Deze informatie kan dus ook zinvol zijn als je regelaar niet zelf gemaakt hebt, maar gekocht hebt. Om de specifieke metingen te begrijpen, die we gaan doen, is het van belang om enkele grootheden uit te leggen / te definiëren:
- Open loop responsie: bij de open loop responsie stellen we de output van de PID regelaar in op een vaste waarde (bijv. 20%) en de responsie van het systeem (in ons geval de HLT temperatuur) wordt gemeten. De term 'open loop' komt van het feit dat we de regellus doorknippen, omdat we een waarde opdrukken. De lus is dus niet gesloten.
- Closed loop responsie: bij de closed loop responsie laten we de PID controller zijn werk doen, terwijl we de setpoint value (de HLT temperatuur referentie) ineens een hogere waarde geven (een stap). We meten vervolgens hoe de PID regelaar functioneert door de HLT temperatuur te meten. Bijvoorbeeld: we verhogen de HLT referentie temperatuur van 20 °C naar 50 °C, we maken dus een stap van 30 °C.
- Dode-Tijd (TD): de dode-tijd van het systeem is de tijdvertraging tussen de initiële responsie en een 10 % verhoging van de proces variabele (wat in ons geval de HLT temperatuur is). De eenheid hiervan wordt gegeven in seconden.
- Relatieve helling (a): de relatieve helling van de stap responsie is de temperatuurverhoging per seconde per procent van de PID regelaar output. Verwoord in een formule: a = temperatuurverandering gedeeld door het tijdsinterval gedeeld door de output van de PID regelaar.
- Versterking (K): de versterking van het HLT systeem. Het HLT systeem kan gezien worden als een systeem met 1 ingang (de PID regelaar output in %) en 1 output (de HLT temperatuur). De versterking van dit HLT systeem is dan gelijk aan de uitgang gedeeld door de ingang, de eenheid hiervan is °C / %.
- Tijdconstante (tau): de tijdconstante van het systeem is een andere belangrijke grootheid van het systeem. Het beschrijft hoe snel of langzaam de temperatuur zal stijgen, gegeven een bepaalde output van de PID regelaar. De eenheid hiervan is seconde.
3.1 Bepalen van de dode tijd en de relatieve helling van het brouwsysteem
Fixeer de output van de PID regelaar op een bepaalde waarde (bijv. 20 %). Bij een grote ketel met veel water erin, is 100 % beter (nauwkeuriger), maar als je de capaciteit van het systeem niet kent, is het beter om met een lagere waarde te beginnen. Nadat de output van de regelaar op een vaste waarde is gezet, zal de temperatuur gaan stijgen en ongeveer de volgende curve volgen:
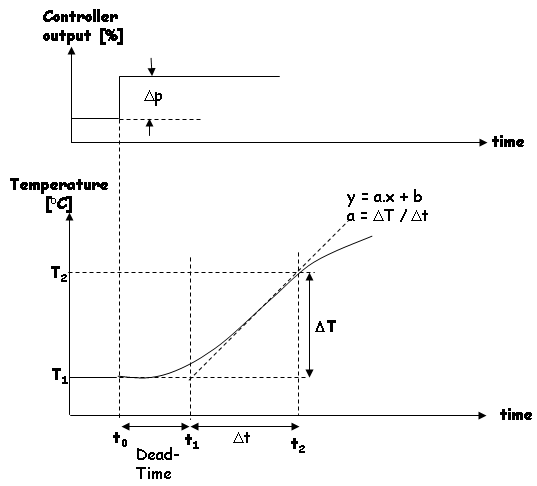
Na het uitvoeren van dit experiment met mijn warmwaterketel (HLT, 90 L water, geen deksel op de pan, PID regelaar output op 100 %, alleen elektrisch verwarmingselement), heb ik berekend dat de dode tijd voor mijn HLT systeem gelijk is aan 115 seconden (zie het document PID Controller Calculus voor details). Tijdens dit experiment, was de temperatuurverandering ongeveer 0.4 °C per minuut (PID regelaar output op 100 %). De relatieve helling is dan gelijk aan 0.004 °C / (%.minuten) of 6.68E-5 °C/(%.s). MAAR... omdat ik recentelijk overgeschakeld ben op nieuwe gasbranders met veel meer vermogen, zal ik dit experiment nog eens moeten herhalen.
3.2 Bepalen van de tijdconstante van het brouwsysteem
Vanwege de grote tijdconstante die meestal in zo'n HLT systeem zit, is het voorgaande experiment niet erg geschikt om de ook de tijdconstante van het systeem te bepalen (niet nauwkeurig genoeg). Dit is dan ook de belangrijkste reden om twee experimenten uit te voeren (theoretisch gesproken geeft het meten van de stapresponsie uit het vorige experiment alle benodigde informatie om de parameters te kunnen bepalen). In dit experiment moet de output van de PID regelaar met de hand op een bepaalde waarde gezet worden (bijv. 20 %). De temperatuur zal nu wederom gaan stijgen en wel volgens deze curve:
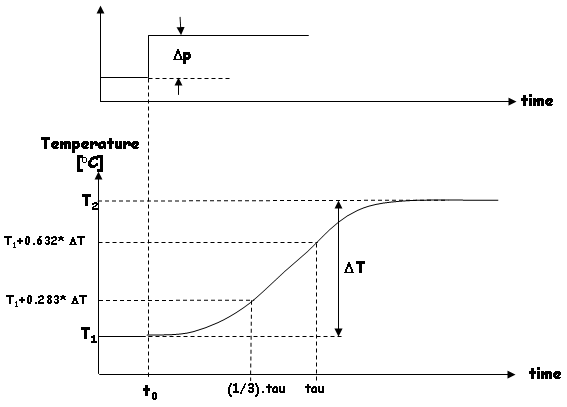
Het verschil met het vorige experiment is dat we nu het HLT systeem naar zijn eindwaarde zullen laten convergeren (in mijn experiment duurde dit het grootste deel van de dag, omdat ik een zo nauwkeurig mogelijke meting wilde hebben). Na het uitvoeren van dit experiment (90 L water, geen deksel op de pan, PID regelaar output op 20 % gezet, alleen elektrisch verwarmingselement), heb ik de volgende data verzameld:
- t0 = 09:49:04, T1 = 19.20 °C
- T2 = 52.99 °C, T2 - T1 = 33.79 °C
- T1 + 0.283 * (T2 - T1) = 28.76 °C. Bekijk de opgemeten grafiek en bepaal wanneer deze temperatuur bereikt werd. In dit experiment werd die temperatuur 6599 seconden na de start (t0) bereikt. Hieruit volgt dat tau/3 = 6599 seconden.
- T1 + 0.632 * (T2 - T1) = 40.56 °C. Bekijk de opgemeten grafiek en bepaal wanneer deze temperatuur bereikt werd. In dit experiment werd die temperatuur 16573 seconden na de start (t0) bereikt. Hieruit volgt dat tau = 16573 seconden.
- Combineer de resultaten van de vorige twee metingen: tau - tau/3 = 16573 - 6599 <=> (2/3) * tau = 9974 <=> tau = 14961 seconden.
- De versterking wordt nu ook direct uit deze data bepaald en wel als volgt: Gain = (T2 - T1) / 20 % = 33.79 °C; / % = 1.69 °C / %.
3.3 Berekenen van de optimale parameters voor de PID regelaar (Kc, Ti en Td)
Om te beginnen, een samenvatting van de gevonden waarden uit de twee experimenten voor mijn HLT systeem:
- Dode Tijd TD = 115 seconden
- Relatieve helling a = 6.68E-5 °C/(%.s).
- Versterking (K) = 1.69 °C / %.
- Tijdconstante (tau) = 14961 seconden.
Er zijn een aantal bekende algoritmen, die de optimale waarden berekenen voor een PI en een PID regelaar. Deze algoritmen berekenen een waarde voor Kc, Ti en Td, die gebaseerd is op de gevonden waarden voor TD, a, K en tau. Deze algoritmen zijn:
- Ziegler-Nichols Open Loop
- Ziegler-Nichols Closed Loop
- Cohen-Coon
- Integral of Time weighted Absolute Error (ITAE-Load): dit algoritme geeft normaliter de beste resultaten. Het foutsignaal wordt geminimaliseerd over de gemeten tijd.
De specifieke formules voor ieder algoritme zijn als volgt:
- Ziegler-Nichols Open Loop:
PID Kc [%/(°C)] Ti [sec.] Td [sec.] 1.2 / (TD * a) 2.0 * TD 0.5 * TD Alleen PI, geen D term Kc [%/(°C)] Ti [sec.] 0.9 / (TD * a) 3.33 * TD - Ziegler-Nichols Closed Loop:
PID Kc [%/(°C)] Ti [sec.] Td [sec.] (1.2 * tau) / (K * TD) 2.0 * TD 0.5 * TD Alleen PI, geen D term Kc [%/(°C)] Ti [sec.] (0.9 * tau) / (K * TD) 3.33 * TD - Cohen-Coon:
PID Kc [%/(°C)] Ti [sec.] Td [sec.] (tau / (K * TD)) * (TD / (4 * tau) + 4 / 3) TD * (32 * tau + 6 * TD) / (13 * tau + 8 * TD) 4 * TD * tau / (2 * TD + 11 * tau) Alleen PI, geen D term Kc [%/(°C)] Ti [sec.] (tau / (K * TD)) * (TD / (12 * tau) + 9 / 10) TD * ((30 * tau + 3 * TD) / (9 * tau + 20 * TD)) - Integral of Time weighted Absolute Error (ITAE-Load):
PID Kc [%/(°C)] Ti [sec.] Td [sec.] (1.357 / K) * [(TD / tau)^-0.947] (tau / 0.842) * [(TD / tau)^0.738] (0.381 * tau * [(TD / tau)^0.995] Alleen PI, geen D term Kc [%/(°C)] Ti [sec.] (0.859 / K) * [(TD / tau)^-0.977] (tau / 0.674) * [(TD / tau)^0.680]
Wanneer deze formules toegepast worden op de gevonden waarden voor mijn HLT systeem, dan worden de volgende resultaten verkregen:
| Numerieke waarden | |||
| Algoritme | Kc [%/(°C)] | Ti [sec.] | Td [sec.] |
| Ziegler-Nichols Open Loop | 156.2 | 230.0 | 57.5 |
| 117.2 | 383.0 | ||
| Ziegler-Nichols Closed Loop | 92.4 | 230.0 | 57.5 |
| 69.3 | 383.0 | ||
| Cohen-Coon | 102.8 | 282.3 | 41.8 |
| 69.4 | 377.2 | ||
| ITAE-Load | 80.8 | 489.0 | 44.9 |
| 59.2 | 810.2 | ||
Al deze oplossingen zijn uitgeprobeerd voor mijn HLT systeem en eigenlijk gaven ze allemaal goede resultaten. Wat wel geconstateerd werd, was dat de D-term nogal gevoelig ingesteld stond, speciaal met de ITAE-Load waarden. Daarom is de D-term nog wat verkleind en heb ik meer filtering toegepast (de constante voor het laagdoorlaat filter heeft nu de waarde 10). Bij Hoe werkt het? kun je een tweetal grafieken zien, die de performance laten zien van de PID regelaar (vooral de onderste grafiek, die is met bovenstaande waarden gemaakt). Na al dit werk, begin ik redelijk te begrijpen hoe de PID regelaar werkt in combinatie met mijn HLT systeem. De werking van de PID regelaar is zodanig goed, dat ik erg blij ben met het resultaat hiervan. Het is grappig om te zien dat het bedenken van dit alles mij maanden gekost heeft, maar dat de uiteindelijke implementatie met slechts een paar regels code te realiseren valt.
Voor de volledigheid nog een aantal bronvermeldingen (een deel van bovenstaande informatie is hiervan afkomstig):
- De site van BESTune voor een beschrijving van de 3 typen PID regelaars (en andere informatie).
- De fantastische (!) User Manual van de DL05 Micro PLC van AutomationDirect.
